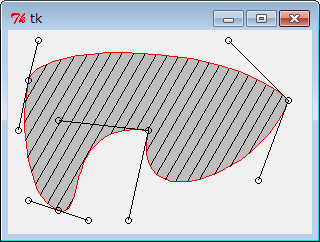
ベジェ曲線パスのストライプ

2019/01/10

Python2.7.8

import math import Tkinter

class Node: p = [0.0,0.0] #self point p0 = [0.0,0.0] #control point p1 = [0.0,0.0] #control point

def __init__(self,p,p0,p1):
    self.p = p
    self.p0 = p0
    self.p1 = p1

class Path: x = 0.0 y = 0.0 nodes = [] closed = False steps = 20

def __init__(self,nodes = None):
    if nodes == None:
        return
    self.nodes = nodes

def points(self):
    if len(self.nodes) == 0:
        return []
    points = []
    points.append(self.nodes[0].p)
    for i in range(1,len(self.nodes)):
        points += self._segment_points(i-1,i)
    if self.closed:
        points += self._segment_points(i,0)
        points = points[:-1]
    return points

def _segment_points(self,i,j):
    points = []
    n0 = self.nodes[i]
    n1 = self.nodes[j]
    pts = self.bezier_curve_points(n0.p,n0.p1,n1.p0,n1.p)
    points += pts[1:]
    return points

def bezier_curve_points(self,p0,p1,p2,p3):
    points = []
    for i in range(self.steps+1):
        t = float(i)/self.steps
        x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
        y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
        points.append((x,y))
    return points

class Pattan: degree = -60 # -90 <= degree <= 90 lines = [] space = 10 def init(self,path): self.path = path self.update()

def update(self):
    #range
    area = [float('inf'),float('inf'),0.0,0.0] #xmin,ymin,xmax,ymax
    for p in self.path.points():
        if   area[0] > p[0]: area[0] = p[0]
        elif area[2] < p[0]: area[2] = p[0]
        if   area[1] > p[1]: area[1] = p[1]
        elif area[3] < p[1]: area[3] = p[1]

    #lines
    lines = []
    sp = self.space
    if self.degree == 90 or self.degree == -90:
        a = 1.0
        b = 0.0
        count = int((area[2]-area[0])/sp+1)
        for n in range(count):
            x = area[0] +sp*n -sp/2
            c = -x
            lines.append((a,b,c))
    else:
        a = math.tan(math.radians(self.degree))
        b = -1.0
        sp = abs(sp/math.cos(math.radians(self.degree)))
        dy = abs(a*(area[2]-area[0]))
        count = int(abs(area[3]-area[1]+dy)/sp+1)
        if a < 0:
            start_y = area[1]-sp/2
        else:
            start_y = area[1]-dy-sp/2
        x = area[0]
        for n in range(count):
            y = start_y +sp*n
            c = -a*x -b*y
            lines.append((a,b,c))
    #cut lines
    self.lines = []
    self.cross_points = []
    nodes = self.path.nodes + [self.path.nodes[0]]
    for line in lines:
        cross = []
        for i in range(len(self.path.nodes)):
            p0 = nodes[i].p
            p1 = nodes[i].p1
            p2 = nodes[i+1].p0
            p3 = nodes[i+1].p
            pts = intersection_of_bezier_and_line((p0,p1,p2,p3),line)
            cross += pts
        self.cross_points += cross #for debug
        if len(cross) % 2 != 0:
            print('error Pattan update()')
            continue
        cross.sort()
        for j in range(0,len(cross),2):
            new_line = cross[j] + cross[j+1]
            self.lines.append(new_line)

def intersection_of_bezier_and_line((p0,p1,p2,p3),(a,b,c)): f0 = a p0[0] + b p0[1] + c f1 = 3 (a p1[0] + b p1[1] + c) f2 = 3 (a p2[0] + b p2[1] + c) f3 = a p3[0] + b p3[1] + c

_a = -f0 + f1 - f2 + f3
_b = 3 * f0 - 2 * f1 + f2
_c = -3 * f0 + f1
_d = f0
if _a == 0:
    if _b == 0:
        if _c == 0: tlist = []
        else: tlist = -_d/_c
    else:
        tlist = quadratic_equation(_b,_c,_d)
else:
    tlist = cubic_equation(_a,_b,_c,_d)
points = []
for t in tlist:
    if t < 0 or 1 < t:
        continue
    x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
    y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
    points.append((x,y))
return points

def cubic_equation(a,b,c,d): p = -b2/(9.0*a*2) + c/(3.0a) q = b3/(27.0*a3) - bc/(6.0a2) + d/(2.0a) t = complex(q2+p3) w =(-1.0 +1j3.0**0.5)/2.0

u = [0,0,0]
u[0] = (-q +t**0.5)**(1.0/3.0)
u[1] = u[0] * w
u[2] = u[0] * w**2
v = [0,0,0]
v[0] = (-q -t**0.5)**(1.0/3.0)
v[1] = v[0] * w
v[2] = v[0] * w**2

x_list = []
for i in range(3):
  for j in range(3):
    if abs(u[i]*v[j] + p) < 0.0001:
        x = u[i] + v[j]
        if abs(x.imag) < 0.0000001:
            x = x.real - b/(3.0*a)
            x_list.append(x)
return x_list

def quadratic_equation(a,b,c): t = complex(bb-4a*c)*0.5 x0 = (-b+t)/(2.0a) x1 = (-b-t)/(2.0*a) return [x0.real,x1.real]

def main(): window = Tkinter.Tk() canvas = Tkinter.Canvas(window,width=300,height=200) canvas.pack()

n0 = Node([20,50],[30,10],[10,100])
n1 = Node([50,180],[20,170],[80,190])  
n2 = Node([140,100],[50,90],[120,190])
n3 = Node([280,70],[250,150],[220,10])

path = Path([n0,n1,n2,n3])
path.closed = True
#n1.p1_avoid = True
#n2.p0_avoid = True
path.pattan = Pattan(path)

if path.closed:
    canvas.create_polygon(path.points(),fill='gray',outline='red')
else:
    canvas.create_line(path.points(),fill='red')
r = 3
for n in path.nodes:
    canvas.create_oval(n.p[0]-r,n.p[1]-r,n.p[0]+r,n.p[1]+r)
    canvas.create_oval(n.p0[0]-r,n.p0[1]-r,n.p0[0]+r,n.p0[1]+r)
    canvas.create_oval(n.p1[0]-r,n.p1[1]-r,n.p1[0]+r,n.p1[1]+r)
    canvas.create_line(n.p[0],n.p[1],n.p0[0],n.p0[1])
    canvas.create_line(n.p[0],n.p[1],n.p1[0],n.p1[1])
for xy in path.pattan.lines:
    canvas.create_line(xy)
#r = 2
#for p in path.pattan.cross_points:
#    canvas.create_oval(p[0]-r,p[1]-r,p[0]+r,p[1]+r)

window.mainloop()

if name == 'main': main()