ベジェ曲線と直線の交点

2019/01/04

Python2.7.8

３次方程式の解を使っての３次ベジェ曲線と直線の交点の算出
（線分の判定はしていない）

# -*- coding: utf-8 -*-

def intersection_of_bezier_and_line((p0,p1,p2,p3),(a,b,c)):
    f0 =      a * p0[0] + b * p0[1] + c
    f1 = 3 * (a * p1[0] + b * p1[1] + c)
    f2 = 3 * (a * p2[0] + b * p2[1] + c)
    f3 =      a * p3[0] + b * p3[1] + c

    _a = -f0 + f1 - f2 + f3
    _b = 3 * f0 - 2 * f1 + f2
    _c = -3 * f0 + f1
    _d = f0
    if _a == 0:
        if _b == 0:
            if _c == 0: tlist = []
            else: tlist = -_d/_c
        else:
            tlist = quadratic_equation(_b,_c,_d)
    else:
        tlist = cubic_equation(_a,_b,_c,_d)
    points = []
    for t in tlist:
        if t < 0 or 1 < t:
            continue
        x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
        y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
        points.append((x,y))
    return points

def line_generalization(p0,p1):
    if p0[0] == p1[0]:
        a = 1.0
        b = 0.0
        c = float(-p0[0])
    elif p0[1] == p1[1]:
        a = 0.0
        b = 1.0
        c = float(-p0[1])
    else:
        slope = float(p1[1]-p0[1])/(p1[0]-p0[0])
        intercept = p0[1] - slope*p0[0]
        a = slope
        b = -1.0
        c = intercept
    return a,b,c

def cubic_equation(a,b,c,d):
    p = -b**2/(9.0*a**2) + c/(3.0*a)
    q = b**3/(27.0*a**3) - b*c/(6.0*a**2) + d/(2.0*a)
    t = complex(q**2+p**3)

    w =(-1.0 +1j*3.0**0.5)/2.0
    u = [0,0,0]
    u[0] = (-q +t**0.5)**(1.0/3.0)
    u[1] = u[0] * w
    u[2] = u[0] * w**2
    v = [0,0,0]
    v[0] = (-q -t**0.5)**(1.0/3.0)
    v[1] = v[0] * w
    v[2] = v[0] * w**2

    x_list = []
    for i in range(3):
      for j in range(3):
        if abs(u[i]*v[j] + p) < 0.0001:
            x = u[i] + v[j]
            if abs(x.imag) < 0.0000001:
                x = x.real - b/(3.0*a)
                x_list.append(x)

    return x_list

def quadratic_equation(a,b,c):
    d = b*b-4*a*c
    if d < 0:
        return []
    if d == 0:
        x = -b/(2.0*a)
        return [x]
    else:
        x0 = (-b+d**0.5)/(2.0*a)
        x1 = (-b-d**0.5)/(2.0*a)
    return [x0,x1]

def bezier_curve(p0,p1,p2,p3,n=20):
    p0_x,p0_y = p0
    p1_x,p1_y = p1
    p2_x,p2_y = p2
    p3_x,p3_y = p3
    points = []
    for i in range(n+1):
        t = i/float(n)
        p_x = (1-t)**3*p0_x + 3*(1-t)**2*t*p1_x + 3*(1-t)*t**2*p2_x + t**3*p3_x
        p_y = (1-t)**3*p0_y + 3*(1-t)**2*t*p1_y + 3*(1-t)*t**2*p2_y + t**3*p3_y
        points.append([p_x,p_y])
    return points

def main():
    import Tkinter
    window = Tkinter.Tk()
    canvas = Tkinter.Canvas(window,width=300,height=200)
    canvas.pack()

    bezier_points = [[10,10],[100,180],[200,10],[290,190]]
    canvas.create_line(bezier_curve(*bezier_points))

    line_points = [[0,20],[300,180]]
    line_eq = line_generalization(*line_points)
    canvas.create_line(line_points)

    xy = intersection_of_bezier_and_line(bezier_points,line_eq)
    r = 3
    for x,y in xy:
        canvas.create_oval(x-r,y-r,x+r,y+r)    

    window.mainloop()

if __name__ == '__main__':
    main()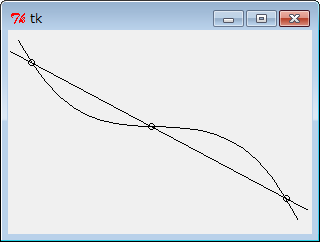

5(その2):直線と曲線の交点(解の公式)
https://pgcity.jp/2010/09/05/175/