ベジェ曲線同士の交点

2019/01/15

Python2.7.8

３次ベジェ曲線同士の交点の算出。
曲線を囲む長方形の重なりを調べ、重なる場合に曲線を２分割することを繰り返して、探索的に交点の近似解を導く方法。

# -*- coding: utf-8 -*-

def intersection_of_bezier_curves(bezier0,bezier1):
    #bezier = p0,p1,p2,p3
    points = []
    buff = []
    buff.append([bezier0,bezier1])
    for n in range(10000):
        bezier0,bezier1 = buff.pop(0)
        xmin0,ymin0,xmax0,ymax0 = bezier_box(*bezier0)
        xmin1,ymin1,xmax1,ymax1 = bezier_box(*bezier1)
        s = (abs(xmax0-xmin0)+abs(ymax0-ymin0)+
             abs(xmax1-xmin1)+abs(ymax1-ymin1) )
        if s < 0.00001:
            x = (xmax0+xmin0+xmax1+xmin1)/4
            y = (ymax0+ymin0+ymax1+ymin1)/4
            points.append((x,y))
        elif not (xmin0 > xmax1 or xmax0 < xmin1 or
                  ymin0 > ymax1 or ymax0 < ymin1): #if overlap
            b0,b1 = bezier_split(bezier0,0.5)
            b2,b3 = bezier_split(bezier1,0.5)
            buff += [[b0,b2],[b0,b3],[b1,b2],[b1,b3]]
        if len(buff) == 0:
            break
    if n == 9999:
        print('Error intersection_of_bezier_curves(): cannot convergence.')
        return []
    #marge
    point_groups = []
    for p in points:
        is_included = False
        for pgroup in point_groups:
            sx = sy = 0
            for tp in pgroup:
                sx += tp[0]
                sy += tp[1]
            x = sx/len(pgroup)
            y = sy/len(pgroup)
            s = abs(p[0]-x)+abs(p[1]-y)
            if s < 0.00001:
                is_included = True
                continue
        if is_included:
            pgroup.append(p)
        else:
            new_group = [p]
            point_groups.append(new_group)
    points = []
    for pgroup in point_groups:
        sx = sy = 0
        for p in pgroup:
            sx += p[0]
            sy += p[1]
        x = sx/len(pgroup)
        y = sy/len(pgroup)
        points.append((x,y))
    print(str(len(points))+' points found.')
    return points

def bezier_box(p0,p1,p2,p3):
    bounds = [[],[]]
    bounds[0] += [p0[0],p3[0]]
    bounds[1] += [p0[1],p3[1]]

    for i in [0,1]:
        a = float(-3*p0[i] +  9*p1[i] - 9*p2[i] + 3*p3[i])
        b = float( 6*p0[i] - 12*p1[i] + 6*p2[i])
        c = float( 3*p1[i] -  3*p0[i])
        if a == 0:
            if b == 0: continue
            tlist = [-c / b]
        else:
            tlist = quadratic_equation(a,b,c)
        for t in tlist:
            if 0 < t < 1: 
                v = (1-t)**3*p0[i] + 3*(1-t)**2*t*p1[i] + 3*(1-t)*t**2*p2[i] + t**3*p3[i]
                bounds[i].append(v)

    return [min(bounds[0]),min(bounds[1]),
            max(bounds[0]),max(bounds[1])]

def bezier_split(points,t):
    if not 0 < t < 1:
        print('Error bezier_split(): t must be 0<t<1.')
        return

    pn = len(points)
    result = [[],[]]
    result[0] = [[0.0,0.0] for i in range(pn)]
    result[1] = [[0.0,0.0] for i in range(pn)]

    result[0][0] = points[0]
    result[1][pn-1] = points[pn-1]

    prev = points
    for i in range(1,pn):
        tmp = [[0.0,0.0] for k in range(pn-i)]
        for j in range(pn-i):
            tmp[j][0] = prev[j][0] + (prev[j+1][0]-prev[j][0]) * t
            tmp[j][1] = prev[j][1] + (prev[j+1][1]-prev[j][1]) * t

        result[0][i][0] = tmp[0][0]
        result[0][i][1] = tmp[0][1]
        result[1][pn-i-1][0] = tmp[len(tmp)-1][0]
        result[1][pn-i-1][1] = tmp[len(tmp)-1][1]

        prev = tmp

    return result

def bezier_curve_points(p0,p1,p2,p3,steps=20):
    points = []
    for i in range(steps+1):
        t = i/float(steps)
        x = (1-t)**3*p0[0] + 3*(1-t)**2*t*p1[0] + 3*(1-t)*t**2*p2[0] + t**3*p3[0]
        y = (1-t)**3*p0[1] + 3*(1-t)**2*t*p1[1] + 3*(1-t)*t**2*p2[1] + t**3*p3[1]
        points.append([x,y])
    return points

def quadratic_equation(a,b,c):
    d = b*b-4*a*c
    if d < 0:
        return []
    if d == 0:
        x = -b/(2.0*a)
        return [x]
    else:
        x0 = (-b+d**0.5)/(2.0*a)
        x1 = (-b-d**0.5)/(2.0*a)
    return [x0,x1]

def main():
    import Tkinter
    window = Tkinter.Tk()
    canvas = Tkinter.Canvas(window,width=300,height=200)
    canvas.pack()

    #bezier_points0 = [[20,10],[160,80],[220,150],[30,190]]
    #bezier_points1 = [[280,10],[60,80],[40,170],[290,180]]
    bezier_points0 = [[20,50],[150,10],[200,190],[280,170]]
    bezier_points1 = [[50,10],[100,150],[200,50],[250,190]]

    cross_points = intersection_of_bezier_curves(bezier_points0,bezier_points1)

    r = 3
    for p in [bezier_points0,bezier_points1]:
        for i in range(4):
            canvas.create_oval(p[i][0]-r,p[i][1]-r,
                               p[i][0]+r,p[i][1]+r,outline='gray')
        canvas.create_line(p[0][0],p[0][1],p[1][0],p[1][1],fill='gray')
        canvas.create_line(p[2][0],p[2][1],p[3][0],p[3][1],fill='gray')

    canvas.create_line(bezier_curve_points(*bezier_points0))
    canvas.create_line(bezier_curve_points(*bezier_points1))

    r = 3
    for x,y in cross_points:
        canvas.create_oval(x-r,y-r,x+r,y+r,outline='red')    

    window.mainloop()

if __name__ == '__main__':
    main()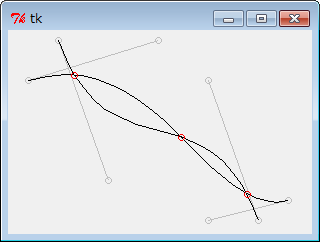

ベジエ曲線の交点について
http://d.hatena.ne.jp/shspage/20140629/1404031123

A Primer on Bézier Curves #Curve/curve intersection
https://pomax.github.io/bezierinfo/#curveintersection

ベジェ曲線の位置の t（0～1）を返すタイプ

# -*- coding: utf-8 -*-

def intersection_of_bezier_curves(bezier0,bezier1):
    #bezier = p0,p1,p2,p3
    position = []
    buff = []
    buff.append([[bezier0,0.0,1.0],[bezier1,0.0,1.0]])
    for n in range(10000):
        temp = buff.pop(0)
        bezier0,t0,t1 = temp[0]
        bezier1,t2,t3 = temp[1]
        xmin0,ymin0,xmax0,ymax0 = bezier_box(*bezier0)
        xmin1,ymin1,xmax1,ymax1 = bezier_box(*bezier1)
        s = (abs(xmax0-xmin0)+abs(ymax0-ymin0)+
             abs(xmax1-xmin1)+abs(ymax1-ymin1) )
        if s < 0.00001:
            position.append([(t0+t1)/2,(t2+t3)/2])
        elif not (xmin0 > xmax1 or xmax0 < xmin1 or
                  ymin0 > ymax1 or ymax0 < ymin1): #if overlap
            b0,b1 = bezier_split(bezier0,0.5)
            b2,b3 = bezier_split(bezier1,0.5)
            c0 = [b0,t0,(t1+t0)/2]
            c1 = [b1,(t1+t0)/2,t1]
            c2 = [b2,t2,(t3+t2)/2]
            c3 = [b3,(t3+t2)/2,t3]
            buff += [[c0,c2],[c0,c3],[c1,c2],[c1,c3]]
        if len(buff) == 0:
            break
    if n == 9999:
        print('Error intersection_of_bezier_curves(): cannot convergence.')
        return []
    #marge
    groups = []
    for t in position:
        is_included = False
        for group in groups:
            d0 = abs(group[0][0]-t[0])
            d1 = abs(group[0][1]-t[1])
            if d0 < 0.00001 and d1 < 0.00001:
                is_included = True
                continue
        if is_included:
            group.append(t)
        else:
            groups.append([t])
    position = []
    for group in groups:
        t = [0,0]
        for _t in group:
            for i in range(2):
                t[i] += _t[i]
        for i in range(2):
            t[i] = t[i]/len(group)
        position.append(t)
    print(str(len(position))+' points found.')
    return position

def bezier_box(p0,p1,p2,p3):
    bounds = [[],[]]
    bounds[0] += [p0[0],p3[0]]
    bounds[1] += [p0[1],p3[1]]

    for i in [0,1]:
        a = float(-3*p0[i] +  9*p1[i] - 9*p2[i] + 3*p3[i])
        b = float( 6*p0[i] - 12*p1[i] + 6*p2[i])
        c = float( 3*p1[i] -  3*p0[i])
        if a == 0:
            if b == 0:
                continue
            tlist = [-c/b]
        else:
            tlist = quadratic_equation(a,b,c)
        for t in tlist:
            if 0 < t < 1: 
                v = (1-t)**3*p0[i] + 3*(1-t)**2*t*p1[i] + 3*(1-t)*t**2*p2[i] + t**3*p3[i]
                bounds[i].append(v)

    return [min(bounds[0]),min(bounds[1]),
            max(bounds[0]),max(bounds[1])]

def bezier_split(points,t):
    if not 0 < t < 1:
        print('Error bezier_split(): t must be 0<t<1.')
        return

    pn = len(points)
    result = [[],[]]
    result[0] = [[0.0,0.0] for i in range(pn)]
    result[1] = [[0.0,0.0] for i in range(pn)]

    result[0][0] = points[0]
    result[1][pn-1] = points[pn-1]

    prev = points
    for i in range(1,pn):
        tmp = [[0.0,0.0] for k in range(pn-i)]
        for j in range(pn-i):
            tmp[j][0] = prev[j][0] + (prev[j+1][0]-prev[j][0]) * t
            tmp[j][1] = prev[j][1] + (prev[j+1][1]-prev[j][1]) * t

        result[0][i][0] = tmp[0][0]
        result[0][i][1] = tmp[0][1]
        result[1][pn-i-1][0] = tmp[len(tmp)-1][0]
        result[1][pn-i-1][1] = tmp[len(tmp)-1][1]

        prev = tmp

    return result

def bezier_curve_points(p0,p1,p2,p3,steps=20):
    points = []
    for i in range(steps+1):
        t = i/float(steps)
        x = (1-t)**3*p0[0] + 3*(1-t)**2*t*p1[0] + 3*(1-t)*t**2*p2[0] + t**3*p3[0]
        y = (1-t)**3*p0[1] + 3*(1-t)**2*t*p1[1] + 3*(1-t)*t**2*p2[1] + t**3*p3[1]
        points.append((x,y))
    return points

def quadratic_equation(a,b,c):
    d = b*b-4*a*c
    if d < 0:
        return []
    if d == 0:
        x = -b/(2.0*a)
        return [x]
    else:
        x0 = (-b+d**0.5)/(2.0*a)
        x1 = (-b-d**0.5)/(2.0*a)
    return [x0,x1]

def main():
    import Tkinter
    window = Tkinter.Tk()
    canvas = Tkinter.Canvas(window,width=300,height=200,bg='white')
    canvas.pack()

    #bezier_points0 = [[20,10],[160,80],[220,150],[30,190]]
    #bezier_points1 = [[280,10],[60,80],[40,170],[290,180]]
    bezier_points0 = [[20,50],[150,10],[200,190],[280,170]]
    bezier_points1 = [[50,10],[100,150],[200,50],[250,190]]

    cross_points = []
    tlist = intersection_of_bezier_curves(bezier_points0,bezier_points1)
    beziers = [bezier_points0,bezier_points1]
    for i in range(2):
        p0,p1,p2,p3 = beziers[i]
        for tpair in tlist:
            t = tpair[i]
            x = (1-t)**3*p0[0] + 3*(1-t)**2*t*p1[0] + 3*(1-t)*t**2*p2[0] + t**3*p3[0]
            y = (1-t)**3*p0[1] + 3*(1-t)**2*t*p1[1] + 3*(1-t)*t**2*p2[1] + t**3*p3[1]
            cross_points.append((x,y))
    r = 3
    for p in [bezier_points0,bezier_points1]:
        for i in range(4):
            canvas.create_oval(p[i][0]-r,p[i][1]-r,
                               p[i][0]+r,p[i][1]+r,outline='gray')
        canvas.create_line(p[0][0],p[0][1],p[1][0],p[1][1],fill='gray')
        canvas.create_line(p[2][0],p[2][1],p[3][0],p[3][1],fill='gray')

    canvas.create_line(bezier_curve_points(*bezier_points0))
    canvas.create_line(bezier_curve_points(*bezier_points1))

    r = 3
    for x,y in cross_points:
        canvas.create_oval(x-r,y-r,x+r,y+r,outline='red')    

    window.mainloop()

if __name__ == '__main__':
    main()